Les filtres.

retour

Qu'est-ce que c'est ?.

Un filtre est un quadripôle qui laisse passer, avec une faible atténuation (inférieure à 3 décibels), certaines fréquences et qui atténue fortement toutes les autres.

Il existe plusieurs types de filtres :

- passe-bas ; laissent passer un plage de basses fréquences
- passe-haut ; laissent passer un plage de hautes fréquences
- passe-bande : laissent passer une bande de fréquences
- saute bande : ne laissent pas passer une bande de fréquence

Si on connaît la fonction de transfert du filtre et sa tension d'entrée, on peut déterminer sa tension de sortie.On définit également le gain G(w) et la phase (w) pour caractériser un quadripôle.

Le gain.

Il s'agit de comparer les valeurs d'entrée du quadripôle et celles de sortie.

le gain en puissance est :

G = Ps / Pe          < 1 pour un quadripôle passif (= non alimenté)

le gain en tension est :

G = Vs / Ve

le gain en intensité est :

G = is / ie

Le quadripôle génère un déphasage entre la tension d'entée et celle de sortie, on utilisera donc les valeurs complexes pour effectuer les calculs.

Fonction de transfert H. (ou transmittance).

C'est une fonction de la pulsation w, on la note H(jw) .

Il s'agit d'une quantité complexe avec :

 

_	js		_	je
Vs =	Vs. e	et	Ve =	Ve . e

 

_	_	_
H(jw) =	Vs /	Ve

Vs et Ve sont les valeurs efficaces des tensions et le déphasage de Vs sur Ve,

_	_	_
H(jw) =	Vs /	Ve

on pose alors :

_		j
H(jw) =	G(w)  /	e

avec G(w) = Vs/Ve , le gain en tension, il représente le module de la fonction de transfert, et (w) = arg = s -je , le déphasage entre Vs et Ve qui représente l'argument de la fonction de transfert.

On a l'habitude d'exprimer le gain d'un quadripôle en décibels ;

g(x) = 20 log G(x)

w est la pulsation, w0 est le facteur 1/ RC et x = w/w0 .

Si on mesure Ve en valeur efficace avec un voltmètre en décibels alors ;

Ve = 20 log Ve/VR en dB

on mesure ensuite Vs = 20 log Vs/VR en dB, ce qui donne :

Vs - Ve = 20 log G en dB

on trace alors g(x) avec en abscisse log x. Le gain et le déphasage sont fonction de la pulsation w du signal d'entrée. Par commodité, on utilise pour le graphe les décades de pulsation : les intervalles [ 1,10 ] [ 10,100 ] [ 0.1, 1 ].

Diagramme de Bode.

On appelle diagramme de Bode les deux courbes :

- G(w) en échelle log-log  
- (w) en échelle semi-log

Ces deux courbes peuvent être obtenues expérimentalement sans connaître la structure du filtre :

- un voltmètre en dB donne le gain pour différentes fréquences (donc pulsations w), on trace G(w) en échelle log-log
- un phasemètre donne le déphasage pour différentes fréquences et on peut tracer (w) en échelle semi-log.

Quelques filtres.

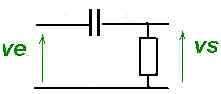
soit le montage RC suivant ;

ve = Ve V2 cos wt

Ce filtre laisse passer, avec une atténuation inférieure à 3 dB, les pulsations inférieures à w0 = 1/ RC.

Les pulsations supérieures à w0 sont très atténuées.

wc = pulsation de coupure = valeur de la pulsation quand w = w0.

Si on utilise le même montage mais que Vs est prise aux bornes de la résistance, on obtient un filtre qui ne laisse passer que les fréquences élevées ; c'est un filtre passe-haut.

soit le montage RLC ;

il est :

- passe-bas aux bornes de C
- passe-bande aux bornes de R
- passe-haut aux bornes de L

dans un montage RLC qui est utilisé en filtre passe-bande, on définit la bande-passante par deux pulsations de coupure telles que :

w = w2 - w1 = w0 / Q et Q = Lw0 / R

Plus w est petit, c'est à dire plus la bande passante est étroite, plus le filtre est sélectif (Q élevé donc Lw0 >>>>R).

La pulsation wc qui sépare le domaine passant du domaine atténué est définie par :

G(w0) = G0 / V2

GdB (wc) = G0dB - 3 dB

Récapitulatif :

montages	(jw)	diagramme de gain	diagramme de phase
RC	= 1/1- j(w /w0) w0 = 1/ RC	pente + 20 dB / décade
RL	= 1/1- j(w /w0) w0 = R/ L
RC	= 1/1+ j(w /w0) w0 = 1/ RC	pente - 20 dB / décade
RL	=1/1+ j(w /w0) w0 = R/ L

 

haut de page